Random Projection

Random Projection is a dimensionality reduction technique that simplifies high-dimensional data while preserving the essential structure of the dataset. By projecting data points onto a lower-dimensional space using random matrices, this method allows for faster processing and reduced model sizes. The key principle behind Random Projection is the Johnson-Lindenstrauss lemma, which ensures that pairwise distances between points are approximately maintained. This technique is particularly useful in applications involving large datasets, such as text and image processing, where computational efficiency is crucial. Overall, Random Projection offers a practical approach to managing complex data while minimizing information loss.

6.6. Random Projection

 Scikit-learn User Guide

The sklearn.random_projection module implements a simple and computationally efficient way to reduce the dimensionality of the data by trading a controlled amount of accuracy (as additional varianc......

📚 Read more at Scikit-learn User Guide
🔎 Find similar documents

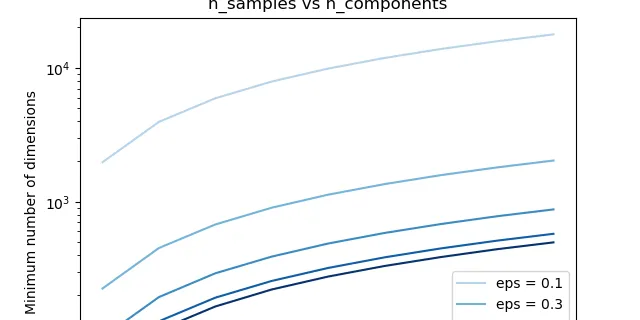
The Johnson-Lindenstrauss bound for embedding with random projections

 Scikit-learn Examples

The Johnson-Lindenstrauss bound for embedding with random projections The Johnson-Lindenstrauss lemma states that any high dimensional dataset can be randomly projected into a lower dimensional Euclid...

📚 Read more at Scikit-learn Examples
🔎 Find similar documents