chi squared distribution
The Chi-Squared Distribution is a fundamental concept in statistics, particularly in hypothesis testing and confidence interval estimation. It arises from the sum of the squares of independent standard normal random variables, making it a special case of the Gamma Distribution. This distribution is widely used to assess how well observed data fit expected data, particularly in tests like the Chi-Squared test for independence and goodness-of-fit. The Chi-Squared Distribution is characterized by its degrees of freedom, which influence its shape and properties, and it is always non-negative, making it suitable for various statistical applications.

Chi-Square Statistic & Chi-Squared Distribution
The Chi-Square Statistic is a number that describes the relationship between the theoretically assumed data and the actual data. It is usually considered as a number or statistic value that verifies…
📚 Read more at Towards Data Science🔎 Find similar documents

Chi-Square Distribution Simply Explained
A simple explanation of the Chi-Square Distribution and its origins Continue reading on Towards Data Science
📚 Read more at Towards Data Science🔎 Find similar documents

Chi-Square Hypothesis Testing in Statistics
Chi-square test is a non-parametric test in hypothesis testing to know the association of two categorical features in bi-variate data or records. Non-parametric tests are distribution-free test…
📚 Read more at Towards AI🔎 Find similar documents
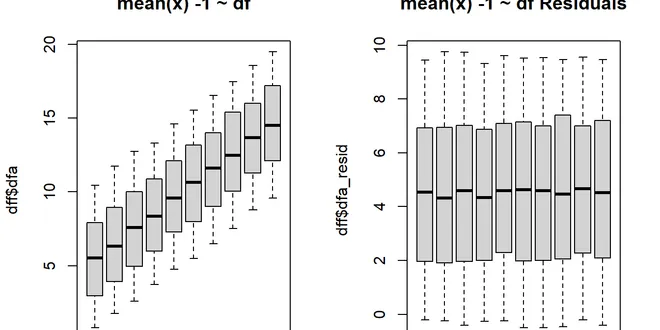
Estimating Chi-Square Distribution Parameters Using R
Introduction In the world of statistics and data analysis, understanding and accurately estimating the parameters of probability distributions is crucial. One such distribution is the chi-square distr...
📚 Read more at R-bloggers🔎 Find similar documents
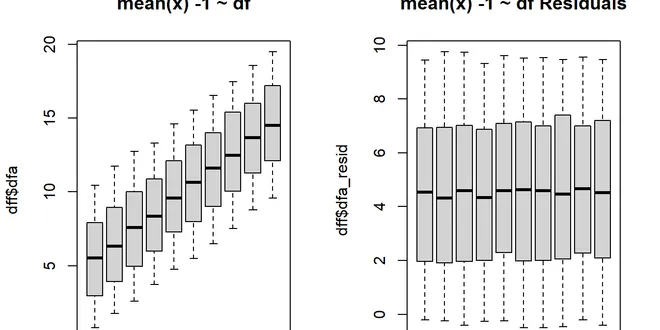
Estimating Chi-Square Distribution Parameters Using R
Introduction In the world of statistics and data analysis, understanding and accurately estimating the parameters of probability distributions is crucial. One such distribution is the chi-square distr...
📚 Read more at R-bloggers🔎 Find similar documents

Chi-Square Test in Machine Learning
Picture a classroom with students choosing between two different activities: reading or playing sports. If you notice more students gravitating toward reading, you might wonder if this is just by coin...
📚 Read more at Towards AI🔎 Find similar documents
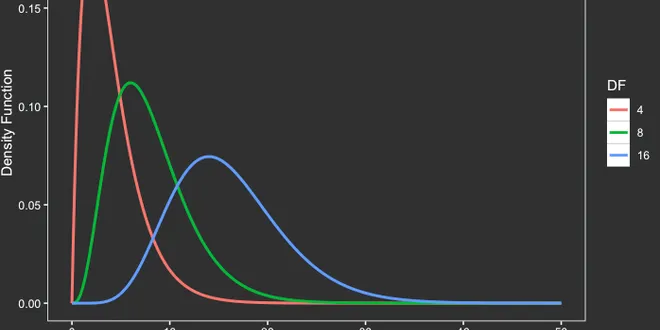
Probability for Data Scientists: The Capable Chi-Squared Distribution
Interactive Visualization of the Distribution Functions Continue reading on Towards Data Science
📚 Read more at Towards Data Science🔎 Find similar documents
Chi-square distribution and test in R
Greetings, humanists, social and data scientists! Was there an association or relationship between gender and the verdicts in investigations in 18th-century London? If an inquest concerned a man, did ...
📚 Read more at R-bloggers🔎 Find similar documents

The Chi-Squared Test Statistic is a Must For Every Data Scientist: A Case Study in Customer Churn
The chi-square statistic is a useful tool for understanding the relationship between two categorical variables. For the sake of example, let’s say you work for a tech company that has rolled out a…
📚 Read more at Towards Data Science🔎 Find similar documents

Chi-Square Test, with Python
In this article, I will introduce the fundamental of the chi-square test (χ2), a statistical method to make the inference about the distribution of a variable or to decide whether there is a…
📚 Read more at Towards Data Science🔎 Find similar documents

Machine Learning: Chi Square Test In Evaluating Predictions
The chi square test is a useful, simple, and easy test to conduct to help gauge the unexpectedness or expectedness of outcomes in data. Included in this post will be the background and circumstances…
📚 Read more at Towards Data Science🔎 Find similar documents

Distributions
In the previous chapter we used Bayes’s Theorem to solve a cookie problem; then we solved it again using a Bayes table. In this chapter, at the risk of testing your patience, we will solve it one mor...
📚 Read more at Think Bayes🔎 Find similar documents

