interquartile
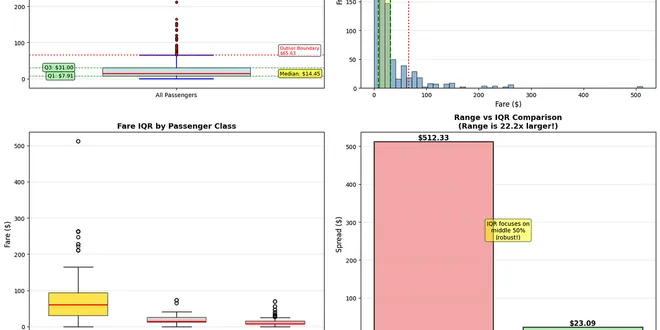
Interquartile Range (IQR): The Outlier Detective That Range Could Never Be
The $512 Ticket Problem You’re analyzing Titanic ticket prices and someone asks: “What’s the typical price range passengers paid?” You calculate the range and proudly report: “From $0 to $512.33!” Bu...
📚 Read more at Python in Plain English🔎 Find similar documents

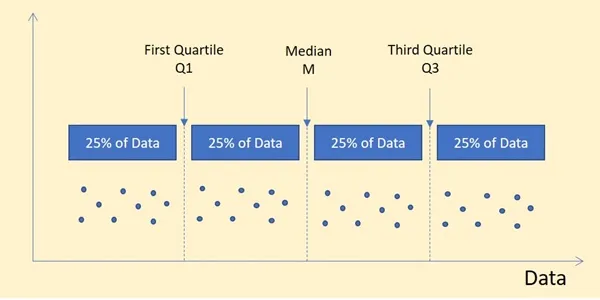
What are quartiles?
We have a sequence with n=12 (numbers from 14 to 57) and let’s imagine these represent the number of tractors some 12 farms have in the northern region of Statistics Land. Quartiles analysis is part…
📚 Read more at Towards Data Science🔎 Find similar documents
How to Easily Forecast the Stock Price Probabilities (Time Series) Using IQR (Interquartile Range)…
I’m not going to dive into the details. You can read a lot about IQR online. Start from Wikipedia if you want to (but you don’t need to). Basically, IQR is the range between 1st and 3rd quartile…
📚 Read more at Level Up Coding🔎 Find similar documents

Solving Quartiles Puzzle with LLM
Ever since becoming an Apple News+ subscriber, I have greatly enjoyed solving the daily Quartiles puzzle. It’s become part of my daily routine and an effective way to relieve stress. I have solved ove...
📚 Read more at Towards AI🔎 Find similar documents
Quartile in Statistics: Detailed overview with solved examples
The post Quartile in Statistics: Detailed overview with solved examples appeared first on finnstats. If you want to read the original article, click here Quartile in Statistics: Detailed overview with...
📚 Read more at R-bloggers🔎 Find similar documents

Experimenting with Quarto
Quarto is the up-and-coming “next generation version of R Markdown” being developed by RStudio. It’s more or less a superset of R Markdown/knitr that’s suited to programming languages besides R. Quart...
📚 Read more at R-bloggers🔎 Find similar documents

Q-Q Plots Explained
In Statistics, Q-Q(quantile-quantile) plots play a very vital role to graphically analyze and compare two probability distributions by plotting their quantiles against each other. If the two…
📚 Read more at Towards Data Science🔎 Find similar documents

Explore Neural Networks Interactively with Quarto Live!
What is Quarto Live? Quarto Live combines Quarto with WebR to enable interactive R code execution directly in the browser allowing for: Running R code directly in the web browser Instant feedback when...
📚 Read more at R-bloggers🔎 Find similar documents

Self-intersecting Quadrilateral
A quadrilateral is a polygon having four sides, four angles, and four vertices. A polygon means that the figure is a closed shape, meaning the last line segment connects back to the first one, effect...
📚 Read more at R-bloggers🔎 Find similar documents
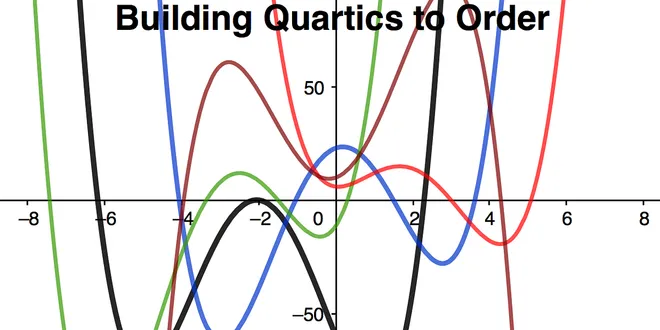
Quartics-Built To Order At Any Address In The X-Y Grid
Build your own Quartic Polynomials to order at any address in the Grid! Continue reading on Towards AI
📚 Read more at Towards AI🔎 Find similar documents

Calculating Quartiles: A Step-by-Step Explanation
Methods for Analyzing and Calculating Quartiles in Python Continue reading on Towards Data Science
📚 Read more at Towards Data Science🔎 Find similar documents
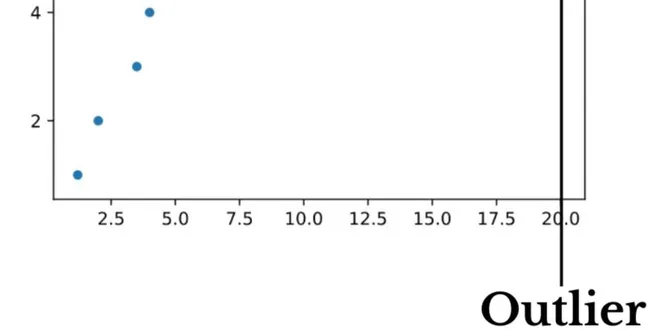
Different Ways To Find Outliers in the Data and How To Remove Them Using Interquartile Statistics.
Different Ways To Find Outliers in the Data and How To Remove Them Using Interquartile Statistics Outliers are the data points or observations far from other data points or very different from other ...
📚 Read more at Towards AI🔎 Find similar documents

